
Keith Edward Bullen was born at Auckland, New Zealand, on 29 June 1906. He attended schools in the Auckland area, completing his schooling at Auckland Grammar School in 1922; he earned recognition as a National Scholar, and was awarded the Eric Astley Prize for mathematics and science and a University Entrance Scholarship. From 1923 to 1925 he was a full-time student at Auckland University College and graduated BA in 1925, his major subjects being pure and applied mathematics. He was first in New Zealand in the final year examinations for the BA degree. In 1925 he became a master at Auckland Grammar School, but continued part-time studies at Auckland University College, being awarded the degree of MA with first class honours in mathematics at the end of 1927. In 1928 he became lecturer in mathematics at Auckland University College, but continued his studies for a BSc degree in physics at the University of New Zealand obtaining first class honours in that degree. In September 1931 he took leave from Auckland University College to study at St John's College, University of Cambridge, returning in 1934 to his post as lecturer and later senior lecturer in mathematics at Auckland University College. The work for his Cambridge PhD was completed while at Auckland. In 1940 he moved to Melbourne, Australia, as senior lecturer in mathematics. He was awarded a special MA degree by the University of Melbourne in 1945 shortly before he was appointed Professor of Applied Mathematics at the University of Sydney, serving in this post until his retirement in 1971. Bullen was awarded an honorary DSc by the University of Auckland in 1963 and another by the University of Sydney in 1976. After his retirement from Sydney he taught at the International Institute of Seismology and Earthquake Engineering in Tokyo and at the University of British Columbia.
Bullen was awarded many medals and honours by societies in Australia and abroad, being elected a fellow of the Royal Society of London in 1949, a foreign associate of the US National Academy of Sciences in 1961, and pontifical academician in 1968. He was a foundation fellow of the ������Ƶ, a member of the Council of the Academy 1955-57, and Matthew Flinders Lecturer and Medallist in 1969.
The William Bowie Medal of the American Geophysical Union was awarded Bullen in 1961, the Arthur Day Medal of the Geological Society of America in 1963, and the Gold Medal of the Royal Astronomical Society in 1974.
Bullen went to St John's College, Cambridge in 1931, and as was customary at that time he began to read for the mathematical tripos. However, Bullen saw little chance of being able to stay at Cambridge for more than two years, nor of being able to return to Cambridge after he had gone back to New Zealand. He was, therefore, anxious to make a start in research while at Cambridge. After a month or two he became a research student, with Harold Jeffreys as his supervisor. Jeffreys was working on the revision of the travel time of the seismic waves from earthquakes and Bullen worked with Jeffreys on this project throughout his years in Cambridge.
At that time the standard travel times used for the determination of the time of origin and of the location of the foci of earthquakes were those of Zoeppritz as modified by H.H. Turner. It was known that there were errors in these tables of as much as 20 seconds. The improvement of travel times is necessarily an iterative process for the earthquake is located using a set of travel times, the residuals from that set of travel times are then used to determine a second set of travel times; the earthquake is then relocated using the second set of travel times, and so on. Iterations of this kind are tedious and time consuming and were especially so in the days of mechanical calculators. It was on tasks such as these that Bullen spent his years in Cambridge. Jeffreys remarks of this period that 'Bullen's energy was phenomenal'.
Bullen's first paper with Jeffreys was a Nature letter on the subject of the corrections to the travel times of P (compressional) waves from earthquakes. It was followed by two papers dealing with the method of calculation of distance in seismology.
The Earth is an oblate spheroid, the polar and equatorial radii being 6356 and 6378 km respectively. In calculating the distance travelled by earthquake waves from a source to the observing station it is necessary to allow for the ellipticity of the Earth. It can be shown that the distance is more accurately determined if the positions of the source and the station are expressed in terms of geocentric latitude (the angle subtended at the centre of the Earth) rather than geographic latitude. This also facilitates model calculations which are carried out for the sphere of volume equal to that of the spheroid. This sphere has a radius of 6371.2 km. Travel time tables too are calculated for this sphere. T'he travel times on the spheroid differ from those on the sphere because of two other effects, the first due to the difference in the lengths of the ray path for the sphere and spheroid and the second because of the ellipticity of the surfaces of equal velocity within the spheroid. The use of geocentric instead of geographic latitudes results in differences in P travel times of the order of a few seconds and the two ellipticity effects mentioned to about 1 second. Both effects are therefore relatively minor. However in calculating the ellipticity corrections it was necessary to determine the variation of density with radius. It was in calculating the density distribution in the Earth as a step towards evaluating the relatively minor ellipticity correction that Bullen made the discovery which established his reputation and became, as he himself said in the preface to The Earth's Density, 'a developing story which has fascinated the author over much of his working life'. I will discuss the ellipticity correction and Bullen's papers on the density distribution within the Earth later in the article.
Bullen returned to New Zealand about the end of 1934, but the collaboration with Jeffreys in the preparation of travel time tables continued until the Jeffreys-Bullen tables were published in 1940. Bullen also published separately an account of the work on the travel times of the phases which had been reflected at the surface of the Earth.
The J-B travel time tables have stood the test of time remarkably well. Beginning about 1960 careful studies in which some systematic effects, for example regional variations in the travel times, have been eliminated have shown that the errors in the travel times from 30° to 100° arc distance are less than about 3 sec. Even now some of the systematic differences have not been satisfactorily determined and explained. At distances between 0° and 20° the observed times in continental shield or platform regions differ from the J-B times as much as 6 seconds. However, it is not yet possible to estimate with certainty how much correction to the J-B tables is required for the average Earth in the distance range 0° to 20°.
Jeffreys showed that the calculation of the ellipticity correction to the travel times of seismic waves involved a term dependent on the ellipticities of the internal strata of equal density (and of course velocity). Adams & Williamson had shown that if any region of the Earth were chemically homogeneous and the seismic velocities Vp and Vs, were known it was possible to calculate the variation of density within that region from the equation
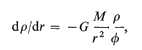
where G is the gravitational constant, M the mass inside the sphere of radius

k being the incompressibility and r the density at radius r. It was pointed out by Birch that equation 1 applied only if the temperature were adiabatic, but the correction required for any conceivable excess of the actual temperature gradient over the adiabatic is very small.
Bullen's procedure was therefore to calculate the mass and the moment of inertia of the crust, then, assuming an initial value for r at the base of the crust of 3.32 gms/cm3 corresponding to dunite, to integrate equation 1 numerically to the mantle-core boundary at a depth of 2900 km. The masses and moments of inertia of the crust and mantle were then subtracted from the known mass and moment of inertia of the Earth to obtain Mc and Ic, the mass and moment of inertia of the core. He found that

where Rc is the radius of the core. This required that the density of the core was greater at the core-mantle boundary than at the centre of the Earth. He remarked that this was 'out of the question both on general grounds and also in view of the strong evidence of lack of rigidity of the central core'. After examining the possible sources of error he concluded that the mantle could not be chemically homogeneous all the way from the crust to the core. In view of seismological evidence for the probable existence of a velocity discontinuity at 400 km he calculated the value of the density at a depth of 400 km required to reduce the constant 0.57 in equation 2 to less than 0.40, the value which applies in the case of a sphere of uniform density. After some further manipulation the density distribution given in column 2 of Table 1 was found. It is interesting to note that this first model of the density variation within the Earth was calculated using Gutenberg's 1929 velocities. This model was the progenitor of the model A series of models, but was never given an identification, nor used by Bullen thereafter.

Once the densities had been calculated it was possible to calculate the variation of g, and of pressure with depth and also the ellipticities of the strata of equal density. It was also possible to determine the variation of the incompressibility and rigidity or shear modulus as a function of depth within the Earth.
Bullen states explicitly that in the 1936 and 1937 papers, 'the hypothesis of a first order discontinuity in density corresponding to the 20° discontinuity was used'. In the 1936 paper he remarks 'the discontinuity being assumed to occur at about 350 km'. In a later paper Bullen stated that the density increase at the discontinuity was 10 percent.
By 1940 Bullen had developed the lettered zonation of the Earth which was the basis of most of his subsequent work on the density variation within the Earth. In the 1940 paper they were as follows:
Layer A: The crust, thickness 33 km
Layer B: Upper mantle, 33-413 km depth
Layer C: Upper mantle transition zone, 413-984 km depth
Layer D: Lower mantle, 984-2400 km depth
In the 1940 paper Bullen followed Jeffreys in regarding the 20° discontinuity as a second order discontinuity, i.e. as a change in the rate of change of velocity with depth rather than the step increase of the 1936 and 1937 papers. The density change was spread throughout region C, hence the name transition zone. In the 1940 paper the density was tabulated down to the core-mantle boundary. It was followed by a paper in which densities were calculated for the core, now split into outer and inner cores and layers E, F and G. The outer boundary radii of layers E, F and G were 3471, 1398, and 1250 km respectively. In the 1942 paper Bullen recognized the uncertainties in the density distribution in the core. Accordingly, he considered two hypotheses:
Quite clearly Bullen regarded these as extreme cases, and in 1942 he tabulated the mean density distribution for the two hypotheses. The individual distributions corresponding to hypotheses (i) and (ii) were first tabulated explicitly in 1947. The 1942 core densities are given in Table 1 as are the density distributions corresponding to the hypotheses (i) and (ii). Bullen remarks, 'The model corresponding to hypothesis (i) has been called model A´; and a model midway between hypotheses (i) and (ii), model A.'
Bullen's work on the density distribution within the Earth established him as one of the leading geophysicists of his era and led during the 1950s to his wielding considerable influence in international geophysics.
In the early 1960s two developments occurred which bore on the density distribution within the Earth and led to Bullen returning to the development of density models for the Earth, the major focus of his early research. One of the constraints on the density distribution within the Earth is the moment of inertia. For many years the accepted value of the moment of inertia, I, was 0.3335Ma2, M being the mass and a the radius of the Earth. Early analyses of the orbits of artificial satellites showed that a significant revision of this relation was required and by 1963 it was clear that I was 0.3308Ma2. It then became necessary to revise the earlier determinations of density.
The second development was that following the great Chilean earthquake of May 22 1960, it was established that free oscillations of the Earth with periods as long as 54 minutes could be observed. The importance of this development was that previously the observational data constraining models of the elastic constants and density within the Earth were, apart from the mass and movement of inertia, the velocities of seismic body waves determined from the travel times of seismic waves. These velocities Vp and Vs, are related to the elastic constants k, incompressibility and m, shear modulus, and the density, r, by the equations:

There are thus two equations for three unknowns. In constructing density models as Bullen had done in the 1930s and 1940s it was necessary to make use of the additional constraint imposed by the use of the Adams-Williamson equation, and assume a value for the density at the top of the mantle selected on the basis of models of the chemical composition of the mantle. The calculated periods of the free oscillations of the Earth depend on the same three quantities, k, r, m, as the velocities Vp and Vs, but not in the same way. The dependence on the three parameters varies with the mode of the free oscillation. Thus a powerful new procedure for testing earth models was available.
Early comparisons for the calculated and observed free periods showed that minor modifications of the density distributions were necessary. It was suggested by MacDonald & Ness that the shear velocity in the lower mantle should be changed, but this modification was not consistent with the observed travel times of S waves. Landisman, Sato & Nafe suggested instead a modification to the density in the lower half of the mantle. This modification was characterized by a super-adiabatic temperature gradient in that region. This was regarded as physically improbable, and Dorman, Ewing & Alsop suggested that the radius of the core should be increased from the Jeffreys value of 3473 km to 3488 km.
Bullen and his graduate student of that period, Ray Haddon, embarked on a lengthy analysis of the models which were in accord with the free oscillation data. The first stage in that analysis was the construction of model A", a modification of model A´ to be consistent with the satellite-derived value of the moment of inertia, 0.3308Ma2. Bullen & Haddon confirmed that if the core radius were increased by 15-20 km the requirement of a super-adiabatic temperature gradient in the lower mantle could be avoided. In a series of papers they developed model HB1. This model fitted the data available in 1967, but not the additional data which became available in the early 1970s. It is quite similar to the model A´ or the first of Bullen's density models in the 1936 paper.
Bullen and Haddon's procedure in developing model HB1 was based on successive approximation. They began with model A" and by trial and error modified the model until the data available were fitted. Bullen remarks that 'an advantage of well-conducted successive approximation over some other procedures is that, broadly speaking, new parameters are introduced into model representations only where statistically demanded by the observational evidence' and that 'the user of successive approximation can always be in close touch with the fine details contributing to the improvements being made.' Other procedures used in the inversion of the observational data were the Monte Carlo procedure and generalized inversion procedures. Bullen thought that Monte Carlo models were 'biased against simplicity' and that a user of Monte Carlo procedures was out of touch with important details of the process because the acceptance or rejection of models was carried out inside a computer.
Generalized inversion procedures do not produce unique models, but for some purposes it is an advantage to have single models corresponding to particular sets of data. Thus generalized inversion procedures have frequently been applied using some additional criteria such as the 'credibility' criterion of Backus and some 'smoothness' requirement. In general the models developed in this way are close to the starting model for the inversion. Almost all starting models derive from, and are close to, Bullen's A models, and thus Bullen's density contributions still dominate our views of the density distribution within the Earth. It is not clear to me, and I am sure Bullen would agree, that the bounds of the acceptable density distributions within the Earth have been explored adequately.
Bullen himself continued to believe that 'successive approximation is likely to be indispensable towards securing the most reliable models, but with [generalized inversion theory] playing an increasing auxiliary role'.
The development of the Bullen density distributions is summarized in Table 1. It is remarkable how similar are the 1936 and HB1 models. In fact even the most recent of the models obtained by inversion of the free oscillation data do not differ very significantly from Bullen's 1936 model.
In 1971 the International Union of Geodesy and Geophysics created a Standard Earth Committee to develop a standard Earth model and appointed Bullen as chairman. Bullen attached great importance to this development and devoted a chapter of The Earth's Density to a discussion of optimum and standard Earth models. Bullen recognized that ultimately a three-dimensional model would be necessary, but he saw the development of a spherically symmetric model in which p, apart from the effect of ellipticity, was a function of r alone, as the immediate goal. He commented that 'many Earth models are being produced which are at best, minor variants of others'. He was frustrated, and in a degree exasperated, because the committee did not make much progress towards the acceptance of a standard model. He remarked:
The task of the committee has proved to be more complex than had been anticipated, partly for the reason that prima donnas performing simultaneously on different keys are slow to produce harmony, partly because of widespread failure to appreciate the difference between a standard and an optimum model.
If he had lived to 1979 he would have been even more disappointed to know that the committee has not yet completed its labours. It is possible, but by no means certain, that finality will be achieved at the meetings of the committee at the General Assembly of the Union in Australia in December 1979.
In 1946 Bullen pointed out in a letter to Nature that the incompressibility k was 6.5 x 1012 dynes/cm2 just above the mantle core boundary and 6.2 x 1012 dynes/cm12 just below. He remarked, 'The suggestion therefore arises that at the very high pressures obtaining in the Earth's deep interior...the compressibility of a substance may be largely independent of its particular chemical constitution.' A number of inferences based on this hypothesis were made, notably that it would follow 'with a high degree of probability that the inner part of the central core below a depth of 5000 km beneath the Earth's outer surface, is solid'. He pointed out that if this were so it might be possible to identify S waves through the inner core and introduced the notation PKJKP for these phases. So far PKJKP waves have not been identified with certainty. However, analysis of free oscillation data has confirmed this suggestion of Bullen's.
In the letter to Nature, Bullen used the phrase 'largely independent of'. Later he wrote 'essentially independent of' and developed a model based upon the hypothesis that k and its derivative dk/dp 'may in the actual Earth change continuously across the core boundary'. This was the basis for the model known as model B, the density for which is given in Table 1.
The hypothesis requires that there should be an abnormally large density gradient in the lowest 200 km of the Earth's mantle (Layer D") and in the Earth's inner core so that these two regions would not be chemically homogeneous.
From 1949 Bullen wrote a number of papers dealing with the constitution of the terrestrial planets. Both Ramsey and Bullen proposed, independently of each other and on different grounds, that the lower mantle material undergoes a phase transformation to a higher density metallic phase of the same chemical composition at the mantle-core boundary. Ramsey's case for this hypothesis rested on solid-state physics arguments whereas Bullen based his support on the fact that using model B it was possible to fit the observed facts not only for the Earth, but also for the other terrestrial planets.
For many years Bullen's research was concerned very much with questions related to the density distributions in the Earth and other planets, and the inferences which could be made if the compressibility pressure hypothesis were valid. These subjects are discussed at length in his book The Earth's Density published in 1975. He was sensitive to the emphasis in this book on his own contributions to the subject and sought to disarm criticism of the book on this score in the preface, writing:
Perhaps I should apologize also for making considerable reference to my own work. I have done this because: first, in a subject rather difficult to expound in all its intricacies, I felt I could contrive the best coherence by basing many of the developments on my own approaches, at least in the first approximations; secondly, I would like this book to help correct numerous recent distortions of detail in my past writings (a phenomenon which of course by no means afflicts only myself in this era of scientist population explosion); thirdly, since the book may be my last major effort on the subject, I have sought to make the account of my work as unambiguous as possible. I hope these reasons will help to counter any suggestion that I regard my contributions are more significant than they really are.
The book will probably be found rather more cautious in its attitude to uncertainties than are many current writings. There is a strong tendency for modern writers (including some notable contributors) in the Earth sciences to be unduly black and white in their pronouncements – rather over-ready to 'prove' and 'disprove' and to declare the 'beliefs' and misbeliefs' of themselves and others in contexts where cautious assessments in terms of probability would be wiser. (This tendency is not confined to the Earth sciences.) Here, I have striven to avoid words such as 'proof', 'true', 'false', 'right', 'wrong', 'valid', 'invalid' except in formal deductive arguments. In inductive arguments, I have sought to 'infer', not 'deduce'; I have been at pains to distinguish between 'mathematical models' and 'facts', not only with density distributions and the like, but also with (so-called) physical 'laws', and so on. Perhaps vainly, I cherish the hope that my pattern of writing may make a modest contribution towards improving the appreciation of some points of scientific inference that need to be specially heeded in geophysics.
The paragraphs quoted reflect Bullen's attitude and philosophy remarkably well. He showed that he was aware of other points of view, he would examine them, he would on occasion modify his own point of view but only if the evidence for so doing was very strong (for example, by 1968 he had recognized that Birch's Murnaghan finite strain theory implied lesser differences in incompressibility as the pressure increased, and he no longer used the compressibility-pressure hypothesis in the narrow sense of the 1949 paper; until this stage was reached he pursued his own concept vigorously).
Bullen's early work on the density distribution within the planets was centred on his compressibility-pressure hypothesis. However, beginning in 1973 he wrote a series of papers which modified a hypothesis of Sorotkin that the Earth's outer core consisted of Fe2O. In Bullen's modification the smaller planets have cores consisting of Fe alone, the intermediate planets outer cores of Fe2O and inner cores of Fe, while the largest planets have cores of Fe2O alone. This hypothesis is of interest because quite recently Ringwood has suggested Fe2O as a possible constituent of the core, though not, as in Bullen's hypothesis, the major constituent.
The section in The Earth's Density dealing with this topic provides another good example of Bullen's philosophy. After discussing models of Mars and Venus based on the Fe2O hypothesis Bullen wrote:
Observational evidence on the seismic velocity distributions in Mars may be forthcoming before too long, and, as with Venus, would assist very much in discriminating between various ideas on the internal structure. It seems desirable to await well-based evidence of this type rather than clutter up the literature with excessive complex speculation. The legions of speculative papers on properties of the Moon, later shown to be quite futile by evidence from artificial satellite observations, provide a salutary illustration.
(Also pertinent is a recent geochemical scramble to produce papers about the Moon's deep interior using data from early samples of materials gathered at the surface. Perhaps it is not too great an exaggeration to liken the scramble to aspiring to infer the Earth's internal structure by digging up one's backyard and performing chemical experiments on the diggings.)
In 1954 there was a series of nuclear explosions at Bikini in the Marshall Islands. Father Burke-Gaffney of Riverview Observatory near Sydney noted that there were pulse-like arrivals on the Riverview records at times which might correspond to the arrival times of the seismic waves from the Bikini explosions. Together he and Bullen explored this possibility. In their first paper they noted that the arrivals from the four blasts were separated by whole numbers of minutes. They argued that this was unlikely unless the shots had been fired at some well defined time, for example, the beginning of the minute. They then showed that using an approximate location based on information in a Gutenberg paper about a 1946 explosion the P travel times at Riverview and other stations which had reported P arrivals in their bulletins were within a second or two of the J-B travel times.
They noted another fact about the bulletin readings for these explosions. At three stations, Pretoria, Kimberley, and Tamanrasset, the PKP readings were all significantly early with respect to the DEF branch in Jeffreys notation (or PKIKP, the phase which had traversed the inner core). Bullen wrote to me and asked me whether the South African records had been misread. Clearly this was not the case. The early arrivals were real and there was a larger amplitude second arrival at about the time expected for PKIKP. Burke-Gaffney & Bullen interpreted these early arrivals as diffractions from the caustic on the BC branch at 142 degrees. Bolt, a student of Bullen at the time of the Burke-Gaffney & Bullen papers, pursued the question of the precursors for some years thereafter. Bolt concluded that the precursor observations could be explained by two successive jumps in velocity in the outer core between 100 and 200 km above the inner core. Other authors proposed even more complex models of the velocity distribution in the lowest 500 km of the outer core as is shown in Figure 12.1 of The Earth's Density. These complex models have been abandoned. The early precursors to PKIKP, first noted by Burke-Gaffney and Bullen, are now interpreted in terms of scattering at the core-mantle boundary, an explanation first suggested by Ray Haddon.
The Bikini explosions occurred while Bullen was president of the International Association of Seismology and Physics of the Earth's Interior. He was greatly impressed by the potential of these large explosions for seismology and in 1955 wrote to the president of the Royal Society of London, and to the Academies of Science in Washington and Moscow proposing 'that for seismological and other experimental purposes one or more atom bombs be exploded during the International Geophysical Year'. He also devoted part of his presidential address to the International Association of Seismology and Physics of the Earth's Interior in 1957 to a plea that information on explosions should be announced timeously so that they could be used for scientific purposes. This plea had an immediate effect for before the meeting ended Bullen received a telegram from the chairman of the US Atomic Energy Commission announcing a forthcoming explosion.
Although his early leaning had been towards pure mathematics it was not long before mathematics had become to Bullen a tool rather than an end. He described himself once 'As an applied mathematician whose work leads him to put context first and mathematics second (but of course a very close second)...' and he remarked upon another occasion:
I think that most of us have met the type of mathematician who is so dazzled by the beauty of his mathematics that he applies it blindly to all and sundry without adequate analysis of the premises on which he bases his deductions, the type whose mind has been made over-rigid by pure mathematics! An important feature of applied mathematics is that it tends to correct this type of mind and, when well taught, to focus needed attention on the problem of initial premises.
Although he gave an address at the inaugural meeting of the Australian Mathematical Society he never became a member of the society and confessed that he had some doubts whether 'it was wise to link applied mathematics with pure mathematics in this middle twentieth century'. However he did regard good training in basic mathematics as essential for the training of applied mathematicians, scientists, and engineers and devoted a good deal of his time to promoting the need for good teachers of mathematics and good training mathematics programmes in schools. As always with Bullen he made his point of view crystal clear. There should be no easy options in mathematics in schools. For a time too, he was Chief Examiner in mathematics for New South Wales. This was no small task to undertake while running a large department and actively engaged in research.
Bullen wrote prolifically. There are 290 papers in his list of publications. The topics are diverse: apart from the many research papers there are scientific biographies, articles in encyclopedias and dictionaries of science, and articles on education, especially mathematical education.
His first book, Introduction to the Theory of Seismology, was published by the Cambridge University Press in 1947 and has been a standard text for seismology ever since. The third edition was published in 1975 and Turkish, Chinese, and Russian translations were published in 1960, 1965, and 1965 respectively. Two other books closely related to his teaching at Sydney, Introduction to the Theory of Dynamics and Introduction to the Theory of Mechanics were published in 1948 and 1949. An eighth edition of the latter was published in 1971. His short monograph, Seismology, was published by Methuen in 1954. The International Institute of Seismology and Earthquake Engineering published his notes for a lecture course on theoretical seismology in 1972. His last book, The Earth's Density, was published in 1975; it covers a wider range of geophysics than its title would suggest because the problem of the Earth's density distribution is so intimately related to seismological information on the interior of the Earth. Surprisingly perhaps there is only one reference to the revolution in the Earth sciences over the past twenty years as a result of which continental drift is generally accepted, and this reference is a casual one in a brief paragraph about the expanding Earth hypothesis.
In spite of the handicap of deafness Bullen played a very considerable role in international geophysics. He served as president of the International Association of Seismology and Physics of the Earth's Interior, as vice-president of the International Union of Geodesy and Geophysics, and as vice-president of the International Scientific Committee for Antarctic Research, and on a number of committees concerned with seismology and geophysics.
He was a very effective member of committees being always well informed on the papers and quietly persistent in discussion. In these activities I sometimes thought that he turned his deafness to advantage for, especially when in the chair, he appeared not to hear remarks which would have diverted discussion to what were, in his view, side issues.
In Australian geophysics too he played a significant role, serving for five years as chairman of the Australian National Committee for the International Geophysical Year and also for five years as chairman of the Australian National Committee for Antarctic Research.
At Sydney he taught courses in all the years of the undergraduate programme. In all his teaching he laid special emphasis on the importance of scientific method and the estimation of the reliability of data by statistical methods. Bullen regarded his role in Sydney as one of training students in all branches of applied mathematics rather than the development of a geophysics school. In his twenty-five years at Sydney he had only two PhD students in geophysics. To some extent this was because he thought it was to the advantage of students to go abroad for specialized training after completing their undergraduate degrees. Many of the students who majored in applied mathematics at Sydney did in fact do so.
Bullen's energy was, as Jeffreys remarked, phenomenal. This was true not only of his vocation, science, but also of his avocations. He was indefatigable as a tourist in his earlier days and later as a coin collector. After long days at scientific meetings, or on committees, he would spend many hours seeking out coin shops or other coin collectors.
He was always kind and courteous at meetings and ever willing to talk to the scientists, young and old, who wished to take advantage of his wide knowledge of seismology and scientific method.
Bullen married Florence Mary Pressley (known as Mary) in Auckland in 1935 and they had two children, John born in Auckland in 1936, and Anne born in Melbourne in 1943.
This memoir was originally published in Records of the ������Ƶ, vol.4, no.2, 1979. It was written by A.L. Hales, Director of the Bernard Price Institute, Geophysical Research University, Witwatersrand (1954-1962); Head, Geoscience Division, Southwest Center for Advanced Studies (later the University of Texas, Dallas) (1962-1973); and Director, Research School of Earth Sciences, Australian National University (1973-1978). Elected to the Academy in 1976.
© 2025 ������Ƶ